Notes For Calculus Life Saver

Chapter 2. Trigonometry

2.1 Basic Knowledge

First, we should review the concept of radian. If we turn round, we say we turn the radian of  instead of rotate 360°. It sounds strange but there is a reason: a circle with a radium of 1 unit has a circumference of   . In fact, the arc length of the sector is exactly the radian of the central angle, according to the picture in the right.

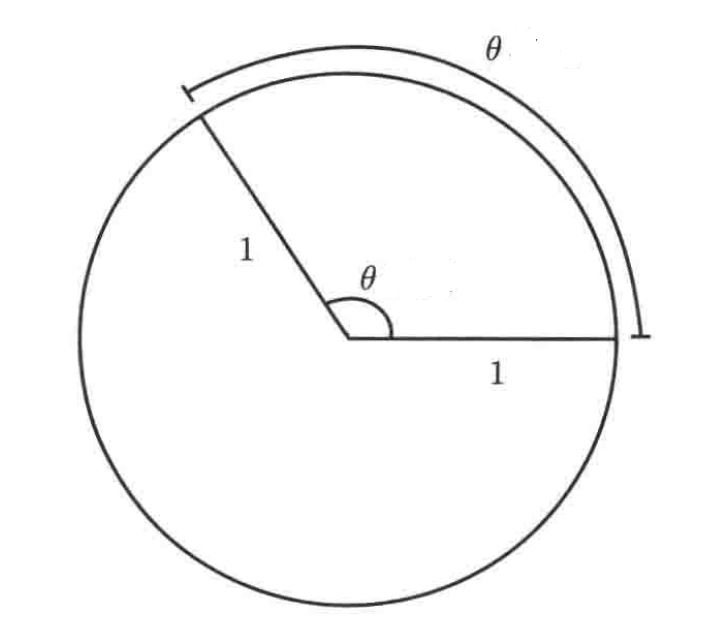
We can use a formula to transform between the angle measured on degrees (a) and the angles measured in radian 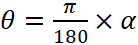：  . Up to now, we have discussed about angles and radian. Now let’s talk about trig functions. Obviously, you have to know how to define trig functions in a right-angled triangle. So, the basic formula is:

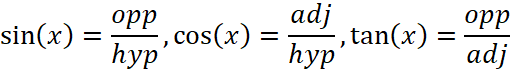
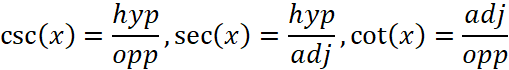
You may have noticed that:

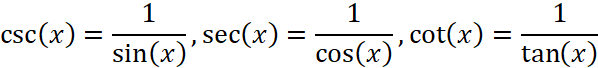
And there are six trig functions: sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), cosecant (csc).