Chapter 2. Trigonometry
2.1 Basic Knowledge
First, we should review the concept of radian. If we turn round, we say we turn the radian of 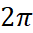 instead of rotate 360°. It sounds strange but there is a reason: a circle with a radium of 1 unit has a circumference of
instead of rotate 360°. It sounds strange but there is a reason: a circle with a radium of 1 unit has a circumference of 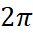 . In fact, the arc length of the sector is exactly the radian of the central angle, according to the picture in the right.
. In fact, the arc length of the sector is exactly the radian of the central angle, according to the picture in the right.
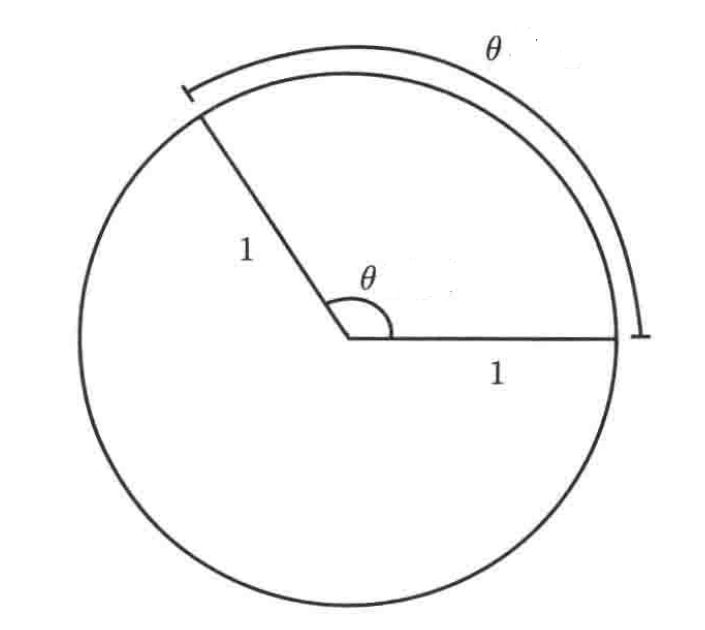
We can use a formula to transform between the angle measured on degrees (a) and the angles measured in radian : 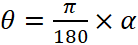 . Up to now, we have discussed about angles and radian. Now let’s talk about trig functions. Obviously, you have to know how to define trig functions in a right-angled triangle. So, the basic formula is:
. Up to now, we have discussed about angles and radian. Now let’s talk about trig functions. Obviously, you have to know how to define trig functions in a right-angled triangle. So, the basic formula is:
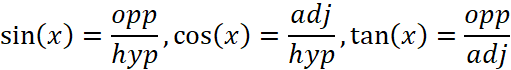
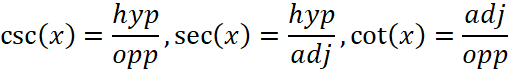
You may have noticed that:
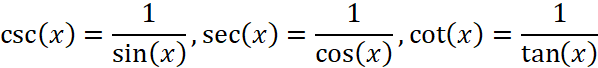
And there are six trig functions: sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), cosecant (csc).
This post belongs to Column 「Notes for Calculus Life Saver」 .
0
comments
latest
No comments yet.