Notes for High School Mathematics

1.2 Additions and Subtractions of Vectors

We can add two vectors together to create a sum vector. Generally, to two non-parallel vectors, we use a method called the Parallelogram Rule or the Triangular Rule. Given the two vectors , how can we calculate their sum?

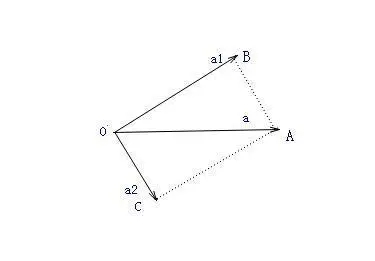
Just like the photo we have showed above, we can simply draw a parallelogram, find its diagonal and we can say (in the second graph) that:

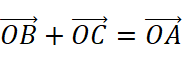
When you move the vector 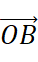 to 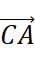 , then you are using the Triangular Rule.

The subtraction is the inverse process of the addition, which also satisfy the Parallelogram and Triangular Rule, but just flip the negative one by 180°.

The addition of vectors has similar properties as the scaler ones It also satisfy the commutative law and associate law of addition.

Commutative Law: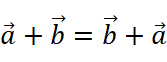

Associate Law: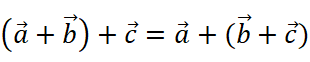

Similar to the Laws of Subtractions in the scalers’ world, we define the subtraction of vectors as the inverse operation of addition.

Question 1: Use the tool of vectors, demonstrate that:

A quadrilateral whose diagonals bisect each other is a parallelogram

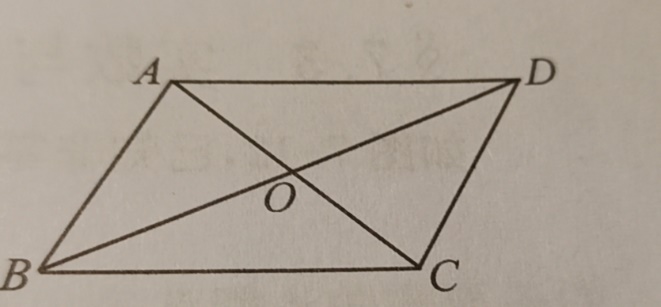
Step 1: Translate it into mathematical language.

Given a quadrilateral ABCD with its diagonals intersect at O. AO=OC, DO=OB

Demonstrate: Quadrilateral ABCD is a Parallelogram.

Proof: According to the information already known:

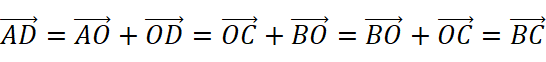∵, and A,D,B,C are not collinear,

∴AD∥BC and AD=BC.

∴Quadrilateral ABCD is a parallelogram.

∴Quad Erat Demonstrandum.