Notes for High School Mathematics

Chapter 1 Plane Vectors

1.1 The Basic Concept of Vectors and their representations

In real life, we meet many mathematical values. Some of them can be represented with just a number like temperature, time, area. Those only have values and have no direction is called a scaler, while those which have either a value and a direction is called a vector. Now that vectors have both a value and a direction, it’s impossible to say which vector is larger.

There are three ways to represent a vector, who are:

1. Arrows
2. Series
3. Matrices

Well, all of you must have learnt about the representation of arrows and their additions and subtractions (if you haven’t, then you must have slept over math class and Mrs.Bao will surely come to blast you). Just take a look at this vector below. How can we represent it?

We represent it as 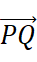.With the former letter represent its starting point and the latter, the ending point. We can also simply write it as .

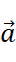As we had said before, a vector has a value (in this case, the length) and a direction. So we can call the length magnitude of the vector, written as 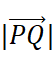. Similarly, we write the magnitude of  as .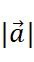

   These are some concepts of plain vectors:

1. Zero Vectors

As I was saying, zero vectors are vectors which have a magnitude of 0. We can represent it as 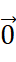. The direction of them can be any directions.

1. Unit Vectors

Like the zero vectors, unit vectors are the vectors whose magnitude is 1. We usually represent them as 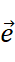. For higher level learners (especially those who have learnt linear algebra), we know that in the Decartes Coordinate System, there are usually 3 perpendicular directions. We call the unit vectors on these directions .

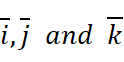1. Parallel Vectors

Parallel vectors are vectors who have the same or inverse directions. (AKA. Collinear Vectors)

1. Equal Vectors

Equal Vectors are vectors whose magnitudes and directions are the same.

1. Inverse Vectors

Inverse vectors are vectors whose direction is 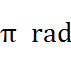 different.