Notes For Calculus Life Saver

3.4 the Limit at ∞ and -∞

There is one more type of limit that we need to investigate. We’ve concentrated on the behavior of a function near a point x = a. However sometimes it is important to understand how a function behaves when x gets really huge. Another way of saying this is that we are interested in the behavior of a function as its argument x goes to ∞. We’d like to write something like：

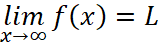
And we use it to represent that when x is really huge, the value of f(x) is really close to L, and it maintain the so-called “close state”.

More importantly when you write down 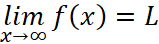, you will surely realize that there is a horizontal asymptote at 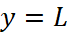. Similarly, when x approaches 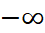, we write something like:

So let’s carry out some definitions.

“The function f has a right hand horizontal asymptote” means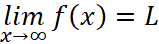

“The function f has a left hand horizontal asymptote” means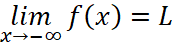

Let’s take a look at this function 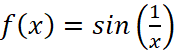. What will happen when x is really large? First of all, when x is really huge,  will be very close to 0, which means will be very close to 0 (since 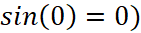. So you can write down this formula with great confidence:

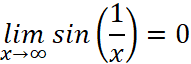
Thus 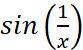has a horizontal asymptote at 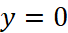. And to our appreciation, we will excitedly figure out that

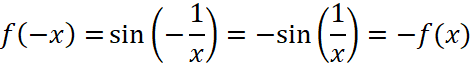
So f is an odd function. We can also say that

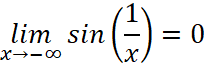
Then you can draw the graph!

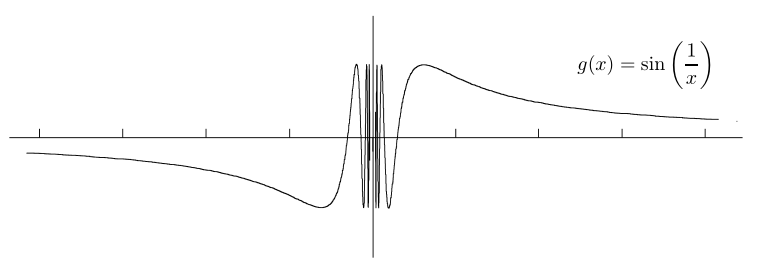
Again, it’s hard to draw what happens for x near 0. The closer x is to 0, the more wildly the function oscillates, and of course the function is undefined at x=0 . In the above picture, I chose to avoid the black smudge in the middle and just leave the oscillations up to your imagination.