Chapter 3 Limits
3.1 the Fundamental Concept of Limit
Suppose we start from the point 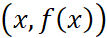 on the function f, and we call it a. When x is really close to a but it is not a, what’s the value of f(x).
on the function f, and we call it a. When x is really close to a but it is not a, what’s the value of f(x).
There is an example here. If the domain of f is 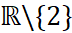 , and
, and
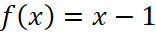
We can also write it like 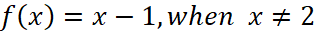 . And the graph of this is like the picture in the right.
. And the graph of this is like the picture in the right.
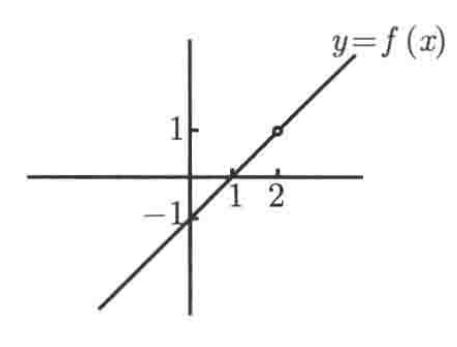
And what’s the value of f(x) when x=2? You may say that when x=2, f(x)=1, and you are wrong because 2 is not in the domain of f. So when x=2, f is not defined. However, on the other hand, what does f(x) approaches when x approaches 2? Another way of saying this is: what happens when x is very close to 2 but doesn’t equal to 2? After several seconds of thinking, you’ll know that when x approaches 2, the value of this function approaches 1. We’ll talk about it specifically in A.1. But now, let’s define the thing happens here:  . Another way of saying this is:
. Another way of saying this is: 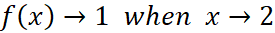 . Now let’s consider another function g. we define that
. Now let’s consider another function g. we define that 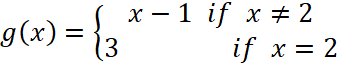
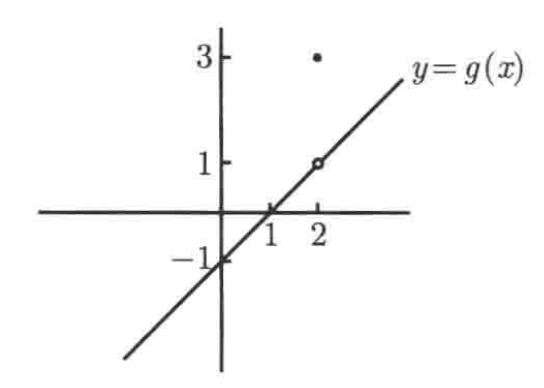
We can draw its graph like the picture in the right.
Now what’s the value of 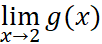 . The key here is that it has no relationship between the limit and the value of g(2). Although g(x) here is 3, we still say that
. The key here is that it has no relationship between the limit and the value of g(2). Although g(x) here is 3, we still say that 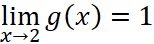 .
.
Another thing we should emphasize is that the variable x here is a dummy variable. It’s just a ephemeral symbol for a number that is really close to 2. We can also write the limit like: 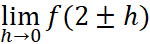 .
.
This post belongs to Column 「Notes for Calculus Life Saver」 .
0
comments
latest
No comments yet.