2.2 Extend the Domain of Trig Functions
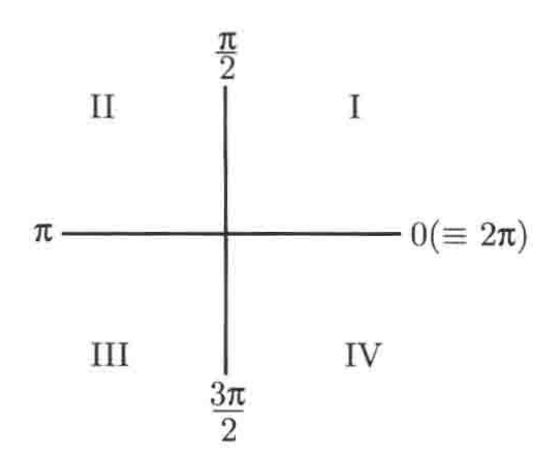
We have to be careful when we take the trig function (for instance tan, cot, sec and csc), because for some x, the function is not defined. For example, 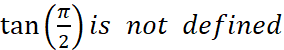 . However, we can take the trig function of almost all angles. First, let’s have a look at the angles from 0 to 2p (remember, p is 360° in degree measurements). In order to be clearer, let’s just draw a rectangular coordinate system with some strange notes on it. The picture is on the right.
. However, we can take the trig function of almost all angles. First, let’s have a look at the angles from 0 to 2p (remember, p is 360° in degree measurements). In order to be clearer, let’s just draw a rectangular coordinate system with some strange notes on it. The picture is on the right.
Noticing that the two axes have cut apart the plane into 4 parts which we wrote Ⅰ,Ⅱ, Ⅲ and Ⅳ here anticlockwise. We call the four parts (again anticlockwise) the 1st to the 4th quadrant.
Imagine you have a point (x,y), and the angle between the line (which passes the point (0,0) and the point (x,y)) is q. We draw a circle which formula is 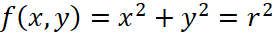 , and we know that the r here is
, and we know that the r here is
 .
.
After we get all this things, we are ready to define our new trig functions:
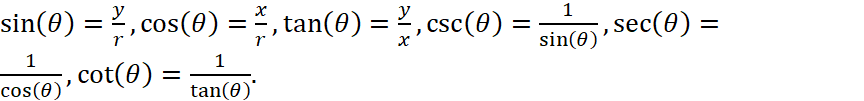
And similarly, we can define the trig functions of the angles which was larger than 2π. 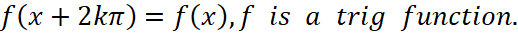 The k here is a positive whole number. And again, we can extend our domain to all real numbers. So
The k here is a positive whole number. And again, we can extend our domain to all real numbers. So 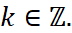
This post belongs to Column 「Notes for Calculus Life Saver」 .
0
comments
latest
No comments yet.